Аддитивные и мультипликативные погрешности
Аддитивной погрешностью называется погрешность, постоянная в каждой точке шкалы.
Мультипликативной называется погрешность, линейно возрастающая или убывающая с ростом измеряемой величины.
Различать аддитивные и мультипликативные п. легче всего по полосе погрешностей.
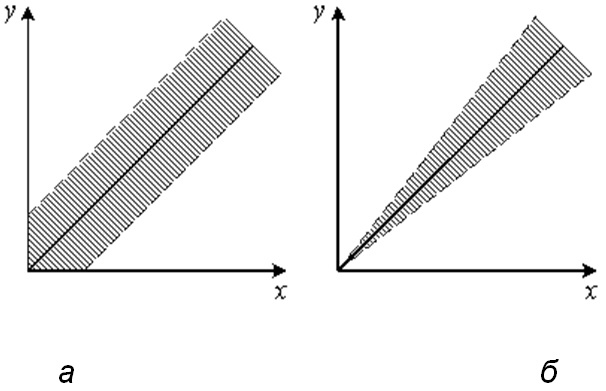Полоса погрешностей
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной п. (рис. а). Иногда такую п. называют погрешностью нуля. Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и п. называется мультипликативной (рис. б). Ярким примером аддитивной п. является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной п.
Для аддитивной п.:
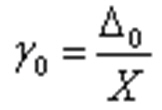Формула для класса точности аддитивной погрешности
где X - верхний предел шкалы, ∆0 - абсолютная аддитивная п.
Для мультипликативной п.:
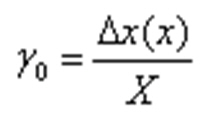Формула для класса точности мультипликативной погрешности
∆x/x=1 - это условие определяет порог чувствительности прибора (измерений).
Абсолютная величина погрешности для обоих типов может быть выражена одной формулой:
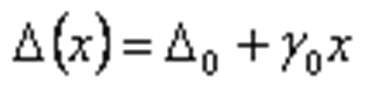Выражение для абсолютной величины
где ∆0 - аддитивная п., y0x - мультипликативная п.
Относительная погрешность с учетом вышесказанного выражается:
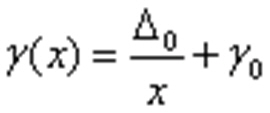Формула для относительной величины погрешности
и, при уменьшении измеряемой величины, возрастает до бесконечности. Приведенное значение погрешности возрастает с увеличением измеряемой величины:
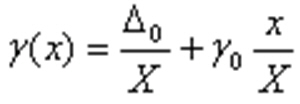Формула погрешности при возрастании величины измерения